Filtre personnalisé - manuel
Le filtre personnalisé requiert ces paramètres :
- nombre de sections et coefficients
- échelle
Pour des informations à propos de ces paramètres voir : -> Filtre IIR - standard-> mise à l’Échelle.
Valeurs des coefficients du filtre , Il est Il est possible d’importer des filtres personnalisés depuis Matlab. Voir : -> filtre Personnalisé importer à partir de Matlab.
De façon générale, les filtres FIR n’ont qu’une seule section. Les filtres à sections multiples peuvent être considérés comme des filtres IIR combinés en un seul (par exemple passe-bas & passe-haut). Cela améliore la stabilité du filtre car les coefficients sont plus petits. Cela dit, il est préférable d’utiliser une seule section pour les filtres personnalisés.
Les lignes du tableau contiennent les coefficients du filtre. Cela définit l’ordre du filtre.
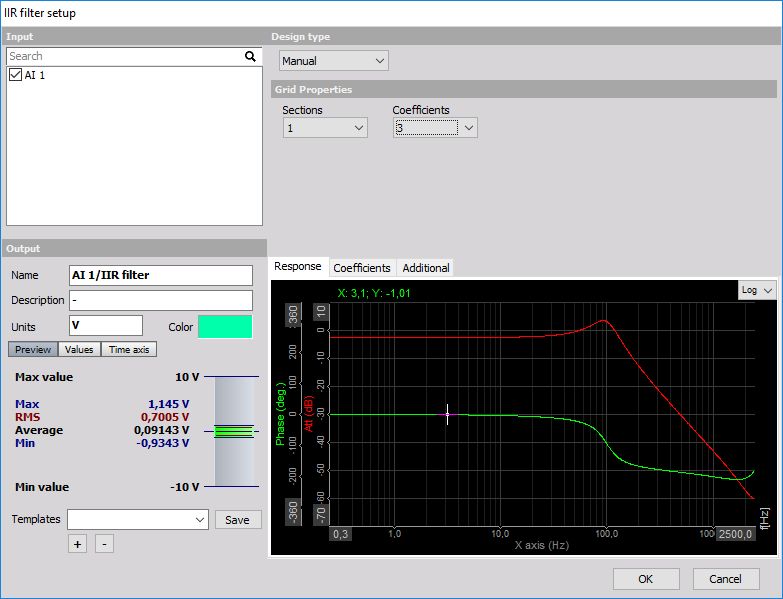
Pour définir les coefficients, entrer a(entrée) et b(reccurr.) et appuyer sur le bouton Mise à jour pour actualiser les paramètres du filtre. Il est également possible de copier/coller les coefficients depuis le presse-papier en faisant un clic droit et en sélectionnant ‘copier vers presse-papier’ ou ‘coller depuis presse-papier’.
La question est désormais : comment définir les coefficients ? La réponse réside dans la connaissance de la construction des filtres dans le plan complexe et la conversion dans le plan réel. Nous allons rappeler rapidement cette procédure.
Normalement, les filtres sont défini dans le plan complexe. Prenons un exemple simple : la formule générale d’un filtre du second ordre :
- \ \$\$H(s) = \frac{g_0 + g_1 s + s\^2}{h_0 + h_1 s + h_2 s\^2}\$\$\
Pour convertir les coefficents dans le plan reel (coefficients dans le domaine temporal) nous aurons besoin d’utiliser une transformation bilinéaire.
- \ \$\$s = 2 f_s \frac{1 + z\^{-1}}{1 - z\^{-1}}\$\$\
où $f_s$ est la fréquence d’échantillonnage. L’équation ci-dessus démontre l’importance des filtres définis dans le plan réel. Ils ne fonctionnent que pour une fréquence d’échantillonnage. Donc si nous avons besoin d’un filtre pour plusieurs fréquences d’échantillonnage, les coefficients doivent être redéfinis.
Si nous remplaçons $s$ dans l’équation (1) par la formule dans l’équation (2), nous aurons pour le numérateur :
- \ \$\$g (1+z\^{-1})\^2 + 2 g_1 f_s (1-z\^{-1}) (1+z\^{-1}) + 4 g_2 {f_s}\^2 (1-z\^{-1})\^2 = \\\\ (g_0 + 2 g_1 f_s + 4 g_2 {f_s}\^2) + (2 g_0 - 8 g_2 {f_s}\^2) z\^{-1} + (g_0 - 2 g_1 f_s + 4 g_2 {f_s}\^2) z\^{-2}\$\$\
Le premier tiers de l’équation est valide pour le coefficient $z^0$, le second pour $z{-1}$ et le troisième pour $z{-2}$ dans le tableau ci-dessus. La partie supérieure de l’équation (avec les coefficients $g$) est valide pour la valeur d’entrée tandis que la partie inférieure (avec les coefficients $h$ est valide pour la partie récursive de l’équation.
Si nous voulons un filtre avec un ordre plus élevé, nous avons besoin de render l’équation similaire à (3) avec un nombre plus important de coefficients. Le résultat aura aussi un facteur $z{-3}$.
Créons à present un exemple simple d’un filtre Butterworth du second ordre. Le prototype dans le plan complexe est :
- \ \$\$H(s) = 1/\left( 1+ \sqrt{2} \frac{s}{\omega_c} + \left(\frac{s}{\omega_c}\right)\^2 \right)\$\$\
où $ω_c$ est la fréquence de coupure en rd/s. Nous devons adapter la fréquence de coupure à la fréquence d’échantillonnage avec :
- \ \$\$\omega_c = 2 f_s \cdot \tan \left( \pi \frac{f_c}{f_s} \right)\$\$\
Si nous écrivons les facteurs pour ce filtre :
- \ \$\$g_0 = 1; \quad g_1=0; \quad g_2 = 0; \\\\ h_0=1;\quad h_1= \frac{\sqrt{2}}{f_c}; \quad h_2=\left( \frac{1}{f_c} \right)\^2\$\$\
Maintenant créons ce filtre :
- fréquence de coupure - f~c~ = 100 Hz
- taux d’échantillonnage - f~s~ = 1000 Hz
Nous devons d’abord faire la pré-déformation:
\ \$\$f_{cp} = 2 \cdot 1000 \cdot \tan \left( \pi \frac{100}{1000} \right) = 649{,}8 \ \frac{\rm{rad}}{\rm{s}} \$\$\
Et maintenant nous devons calculer les coefficients pour les parties directes et récursives du filtre avec les facteurs de substitution (6) de l’équation (3) :
| $a(z^{0}) = 1+0+0 = 1$ | $b(z^0) = 1 + 2 \cdot \sqrt{2} \cdot \frac{1000}{649{,}8} + 4 \cdot \frac{10002}{649{,}82} = 14{,}825$ |
| $a(z^{-1}) = 2 \cdot 1-0 = 2$ | $b(z^{-1}) = 2 \cdot 1 - 8 \cdot \frac{10002}{649{,}82} = -16{,}944$ |
| $a(z^{-2}) = 1-0+0 = 1$ | $b(z^{-2}) = 1 - 2 \cdot \sqrt{2} \cdot \frac{1000}{649{,}8} + 4 \cdot \frac{10002}{649{,}82} = 6{,}12$ |
Finalement, nous définissons le nombre de coefficients à 3, le nombre de section à 1 et entrons les 6 valeurs calculées dans le tableau puis pressons sur mise à jour.
Gardons en mémoire que ce n’est valide que pour une fréquence d’échantillonnage de 1kHz. Pour d’autres fréquences, nous devrons recalculer les coeffecients.
Créer un filtre Butterworth du second ordre est plus facile avec les filtres standards de DEWESoft mais si nous avons besoin d’un filtre spécifique, il est nécessaire de le faire à la main.
Le chapitre suivant décrit comment importer des filtres personnalisés depuis Matlab.