Filtre Standard
Un filtre standard permet essentiellement de filtrer un signal en fréquence en le limitant vers le haut, le bas, en passe-bande et en réjecteur.
Les réglages des Filtre RII vous permettent de paramétrer:
- Un Type et un Prototype
- Un Ordre
- Une Fréquence de coupure
- Une limite d’ondulation
- Un coefficient de mise à l’échelle
Vous pouvez visualiser l’effet de ces paramètres directement sur le diagramme de Bode / et la représentation sur plan complexe des Pôles et Zéros. Pour le type vous pouvez définir : passe-bas, passe-haut, passe-bande, réjecteur pour différents prototypes.
Type de Filtre
Vous pouvez sélectionner le type de Filtre parmi les éléments proposés de la liste:
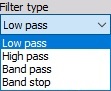
- Passe-bas - filtre qui élimine la présence de hautes fréquences dans votre signal.
- Passe-haut - filtres qui élimine la composante DC et les basses fréquences.
- Passe-bande - filtre laissant passer les signaux en amplitude dans une seule bande de fréquence.
- Réjecteur - La bande de réjection des fréquences du signal est à définir - une seule section possible.
Prototype du Filtre
Vous pouvez sélectionner le Prototype du filtre parmi ces éléments :
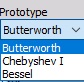
- Butterworth - Prototype offrant une réponse en amplitude linéaire dans la bande passante. Il conserve une bonne forme d’onde du signal entrant, même avec des ordres élevés. L’atténuation est définie par la formule \$(-20 \frac{dB}{décade} \times ordre)\$.
- Chebyshev - Parfois la selection des filtres est définie par l’application en cours, mais en général, le prototype Chebyshev donne des meilleurs résultats. Cependant, il ne conserve pas la forme pour un ordre élevé et il ondule dans la bande passante.
- Bessel Le prototype Bessel possède une réponse linéaire maximale. Ses performances s’en trouvent cependant amoindries.
Ordre
L’ordre du filtre est sélectionnable depuis la liste déroulante. L’ordre définit “l’agressivité” du filtre. Pour un filtre Butterworth, la formule de l’atténuation est : \$(-20 \frac{dB}{décade} \times ordre)\$, donc pour l’ordre 6, la pente serait \$-120 \frac{dB}{décade}\$ cela signifie que si l’amplitude à 100Hz (dans la bande de rejection) est 1, l’amplitude à 1000Hz serait 1E^-120/20^ = 1E − 6.
Plus l’ordre du filtre est élevé, plus la puissance de calcul nécessaire est élevée. Il faut faire 6 multiplications supplémentaires par couple de 2 ordres ajoutés.

Fréquence de coupure
La fréquence de coupure d’un filtre définit le point à -6dB d’amplitude (moitié de l’amplitude) du filtre. Il est possible d’entrer la fréquence de coupure dans le champ de saisie :
- Fc1 - Fréquence basse
Entrer Fc1 pour filtres passe-bas, passe-bande et réjecteur.
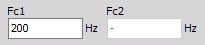
- Fc2 - Fréquence haute
Entrer Fc2 pour filtres passe-haut, passe bande et réjecteur.
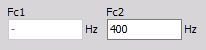
- Fréquence haute et basse
Entrer Fc1 & Fc2 pour filtres passe-bande et réjecteur.
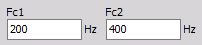
La valeur de fc1 doit toujours être inférieure à Fc2. Ces valeurs sont limitées par la stabilité du filtre. Dans DEWESoft, les filtres sont calculés par section, ce qui permet d’avoir un ratio de 1 pour 100000 entre la fréquence de coupure & la fréquence d’échantillonnage. Il est donc possible de calculer un filtre passe-haut de 1Hz avec une fréquence d’échantillonnage de 100kHz.
Ondulation
Il est également possible de définir l’ondulation. L’ondulation est l’erreur maximale d’amplitude du filtre dans la bande passante en dB.
REMARQUE: Ce champ de saisie n’apparaît que pour le prototype Chebyshev.
L’échelle
Il est possible enfin de définir l’échelle du filtre. Le facteur d’échelle signifie que le dernier facteur de la multiplication est écrit dans la valeur de sortie. Cela permet de modifier l’unité par exemple. Un bon exemple pour illustrer l’échelle est écrit dans la section Intégrale.
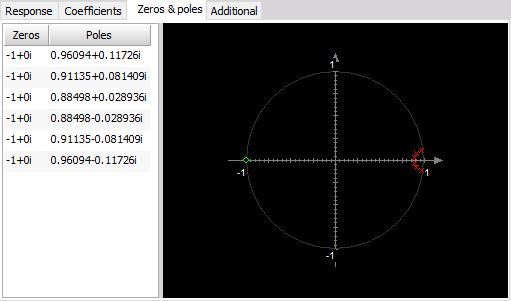
Courbe de réponse / Prévisualisation Zéros Et Pôles
En bas de la fenêtre de configuration, on peut voir quelques graphiques utiles représentant le filtre fraîchement créé. Premièrement il y a la courbe de réponse.
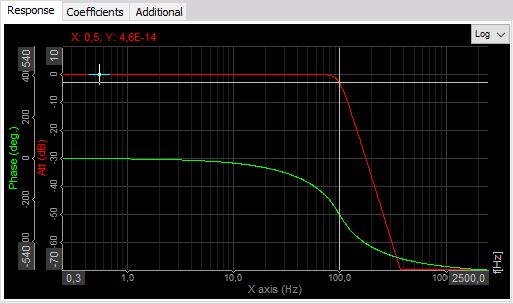
La courbe rouge représente l’atténuation en amplitude du filtre en dB en function de la fréquence. Pour rappel, l’échelle en dB est calculée selon : *$a [dB] = 20 \times log_{10}(A)$, , donc le ratio d’atténuation est calculé grâce à \$A=10\^\frac{a}{20}\$.
Si la valeur d’atténuation est -34dB, le ratio entre l’entrée et la sortie à cette fréquence est : A=10\^(-34/20)=0,02. Donc si l’entrée est un signal sinusoidal d’amplitude 1V, le signal filtré sera un signal sinusoidal d’amplitude 0.02V.
La phase montre le retard du signal en degrés.
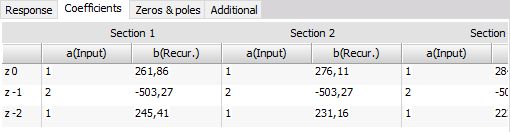
Le tableau au bas de la fenêtre montre les coefficients grâce auxquels le filtre sera calculé. Le filtre est séparé en plusieurs sections pour une stabilité optimale. Le résultat de la première section est utilisé pour la seconde et ainsi de suite. Ces coefficients peuvent également être copiés / collés en faisant un clic droit sur le tableau.
Sur l’aperçu de la courbe, vous pouvez choisir un affichage linéaire ou logarithmique, éditer les valeurs des coordonnées et faire une mise à l’échelle automatique de l’axe des ordonnées.
Le diagramme zéros & poles montre la position des zéros et des pôles du filtre et permet de se faire une idée de la stabilité du filtre.