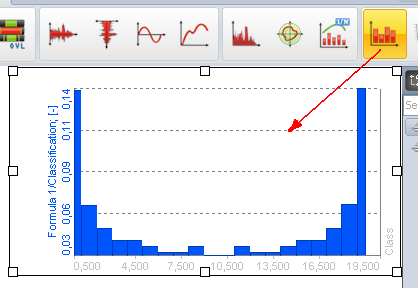
Classification

La fonction de classification permet de compter les valeurs d’une voie de mesure et de les assigner à des classes. Par exemple, une classification que nous avons quasiment tous fait à l’école primaire, était de trier les élèves de chaque classe selon leur poids ou leur taille.

Dans le domaine de la mesure, la classification est utilisée pour des applications diverses : trouver la distribution des fréquences de la grille d’électricité par rapport au temps, ou bien trouver la distribution d’exposition aux niveaux sonores de zones particulières.

Premièrement, nous avons besoin de définir le résultat attendu de la classification. Il y a trois options :

• Basé sur valeur unique - Le résultat sera un unique tableau contenant les données du processus en entier
• Basé sur bloc - Le résultat sera un set de tableaux chacun ajouté à la suite des blocs définis. Par exemple si l’on a une taille de bloc de 2 secondes et qu’on acquiert des données pendant 10 secondes, il y aura 5 tableaux de valeurs classées chacun valide pour 2 secondes de données.
• En continu - Le résultat final sera une somme d’une suite de valeurs qui aura été mis à jour chaque fois qu’une nouvelle valeur est ajoutée à la suite.
• Classes dans voie séparée - Cette option créera des voies valeurs unique pour chacune des classes. L’affichage dans un multimètre est parfait pour cette option.

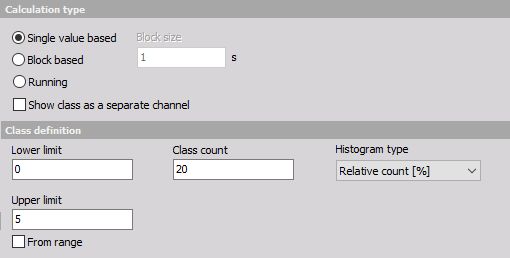
Pour la définition des classes nous devons définir :

• Limite basse - Défini la limite basse de début de comptage - toutes les valeurs en dessous de cette limite seront comptées dans la première classe.
• Limite haute - Défini la limite haute de fin de comptage - toutes les valeurs au-dessus de cette limite seront comptées dans la dernière classe.
• Nombre de classes - Défini le nombre de classes. Dans l’exemple ci-dessus, la largeur de chaque classe sera 5/20=0.25. La première et la dernière classe auront une largeur réduite de moitié c’est-à-dire de 0 à 0.125. La 2ème aura une valeur médiane de 0.25 et ira de 0.125 à 0.375 et ainsi de suite.

Le type d’histogramme défini l’amplitude de sortie des données :

• Comptage absolu - Le nombre d’échantillons par classe augmente en permanence.
• Comptage relative - Le nombre d’échantillons par classe est normalisé par rapport au nombre total d’échantillons comptés (la somme de toutes les classes sera toujours 1).
• Comptage relatif[%] - Identique au comptage relatif, mais exprimé en pourcentage (la somme des classes sera toujours 100).
• Densité - Fourni la densité empirique de probabilité. Le nombre d’échantillons par classe est normalisé par rapport au nombre total d’échantillons comptés et divisé par la taille de classe. Dans ce cas, les valeurs ne dépendent pas du nombre de classes dans une gamme.
• Densité [%] - Identique à la Densité, mais multiplié par 100
• Distribution - Fourni la distribution empirique de probabilité. Chaque classe contient la somme de toutes les classes inférieures et le nombre d’échantillons actuel, normalisé par rapport au nombre total d’échantillons. La classe la plus haute a une valeur de 1.
• Distribution [%] - Identique à la Distribution mais exprimé en pourcentage. La classe la plus haute a une valeur de 100.

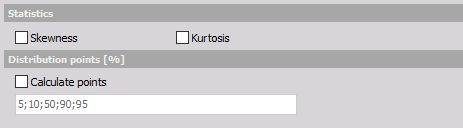
Il existe également d’autres voies de sortie spéciales. L’asymétrie (skewness) de la distribution de probabilité et la Kurtosis (mesure des pics de la distribution). De plus, on peut avoir une liste des valeurs des points de la distribution. Les points de la distribution sont les valeurs des classes auxquelles la distribution atteint la valeur entrée.

Pour le moment, les points de distribution fonctionnent seulement si la distribution est de type histogramme.

Les histogrammes peuvent être affichés dans un graphe 2D en Mesure et en Analyse.

Si nous choisissons un calcul basé sur bloc, on peut aussi utiliser le graphe 3D pour afficher l’historique des classifications.