Short-time Fourier transform
STFT is a well-known technique in signal processing to analyze non-stationary signals. STFT is segmenting the signal into narrow time intervals and takes the Fourier transform of each segment. In Dewesoft’s FFT setup you can set FFT’s resolution, Window, and Overlap and for better understanding what that means, let’s look at the picture below. Window size depends on FFT’s resolution, we can just say FFT size (representing a segment of a signal).
Why use STFT? Relationship between acquisition time T and frequency resolution df is
$\large\frac{1}{T}=df$,
where $df=\frac{sampleRate}{2 FFTsize}$. A smaller time frame, T will result in poorer frequency resolution (bigger df). When the signal changes fast, you need a small T to calculate the frequency spectrum faster. but you still want better frequency resolution and here STFT comes in place.
STFT Block size long segment of signal in time domain, let’s say $Block size = 64$ and sample rate = 2000. Currently, frequency resolution would be $df=\frac{2000}{2*64}$. Now we will use the desired $FFT size$, that you set in STFT setup to improve df, take $FFT size = 1024$. We employ frequency interpolation and obtain FFT size long block. We can say, frequency interpolation in the time domain results in an increased sampling rate in the frequency domain. Here frequency interpolation increased our frequency-domain sampling (resolution) by a factor of 16 (1024/64), i.e.
$\large df= \frac{2000}{2\cdot64\cdot16}=\frac{2000}{2\cdot1024}$
We get 16 times better frequency resolution for the same time frame.
For example, FFT (red) and STFT (blue) of speech waves are shown below. FFT has a resolution of 2048 lines, Blackman window, and 50% overlap and STFT also has Block size 2048, FFT size 16K, Blackman window used, and 50% overlap. As we can see, STFT performs better with the same block size (but more calculated lines). We improved frequency resolution for the same amount of scooped data. In most cases here, FFT does not strike center frequencies (peaks), which are usually wanted results.
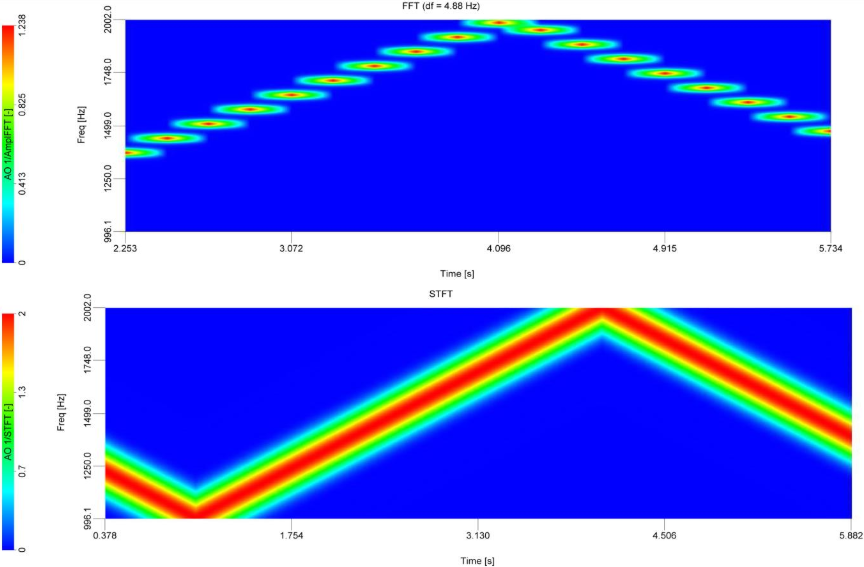
The next example compares, how STFT and FFT perform with the signal, where frequency changes fast over
time. Here, frequency changes in a loop from 1000Hz to 2000Hz in 3 seconds. In first 3D graph is used FFT (1024 lines) and we can see, that we have gaps between frequency spectrums, but in measured data, frequency changes continuously over time. The second 3D graph shows STFT (Block size = 64, FFT size = 1024 and 0% overlap), where there are no gaps and frequency traces are connected. If you look closely, there is a difference in the time frame on 3D graphs between STFT and FFT. STFT has smaller time frames, consequently, the frequency spectrum moves smoother over time, therefore it is more accurate.
- Block size - defines the number of real data samples to be taken for the calculating FFT.
- FFT size - defines the number of resulting lines and with that the ratio between real and zero padded lines.
- Window type - describes the FFT window to be used. There is a good description of the usage of different window functions in the tutorial. By default\, we use Blackman, because it is a good compromise between the amplitude error and width of sidebands.
- Overlap - defines how much will two FFT shots overlap between each other. 50% is enough that all the samples will have the same weight as the result independent of the window which is used.
STFT can be viewed in 2D or 3D graphs.