Integration and double integration
Integration
There are two main purposes of integration: first is to get for example traveled distance from measured velocity or to get the energy from measured power. Another type of integration is to calculate the velocity vibration from the measured acceleration.
A clear difference between two basic functions is that in the first application the carrier of information is the DC value - the offset (traveled distance or spent energy). In other application the offset is only a measurement error and the carrier of information is the dynamic part of the signal-vibration velocity in our example.
1. Let’s first take a look at how to integrate distance from velocity. If we have for example velocity in km/h as an input channel, we choose a filter, integration, and switch OFF the option to ‘Filter low frequencies and DC’. Now the only thing left is to define the Scale. We have to know that integration adds a sec to the unit.
EXAMPLE: So if we have km/h as input, we have at output: km/h * sec = 1000 m / 3600 sec * sec = 0.278 m.
Therefore if we want to have the output in meters, we have to enter 0.278 as the scale factor. If we want to have output in km, we have to enter 0.000278.
2. Let’s practice on another example - if we have input channel as a power in kW, we have at the output:
EXAMPLE: kW * sec=kW * 1/3600 * h=0.000278 kWh - this is our scaling factor.
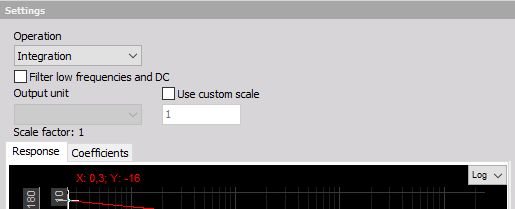
The second application is to use integration on dynamic signals like vibration acceleration. If we have measured acceleration, there is always some offset because of an amplifier and AD converter offset. This offset will result in a drift of result, which is not wanted in this case. Therefore we need to use the option ‘Filter low frequencies and DC’ to cut this offset.
NOTE: The single- and double integration calculations are first and second order filters respectively, designed after the Trapezoidal integrator rule. Enabled high-pass filtering for integration is a Butterworth filter type
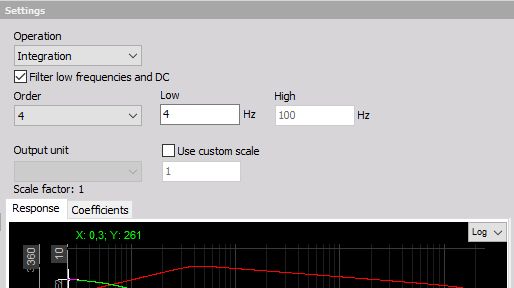
Then we need to define the Order. Be aware that integration is equivalent to filter with order 1, so we need to choose a high pass filter with order 2 or higher to really cut DC values. The Flow tells us where the resulting velocity will be cut off. High values of Flow (like 10 Hz) will result in very fast stabilization in the case of overload, but it might on the other side already cut the information we require. Low values (\< 1Hz) will result in quite slow stabilization times (typically 5÷10 seconds for 1 Hz filter) but will pass through the virtually entire frequency range.
For vibration measurement, the usual value is from 3 to 10 Hz for general purpose measurement. For low-frequency vibration like the human body or building vibration, a value between 0.3 and 1 Hz is used. For special application, like sea sickness or high structures (like TV towers or cranes) movement a very low frequency like 0.1÷0.3 Hz is used, but we have to know that the stabilization will be a very long process. In this case, we also need to assure that the sensors we are using have such low-frequency range. General purpose ICP sensors have the cutoff frequency between 0.3 to 1 Hz and therefore are not useful in such applications.
Let’s look at the Scale - scaling factor for this application. Let’s assume that we measure the acceleration in g. If we want the results in mm/s, we need to have a scaling factor:
1 g * sec = 9,81 m/sec/sec * sec = 9,81 m/s = 9810 mm /s
So we need to enter 9810 in the field scaling.
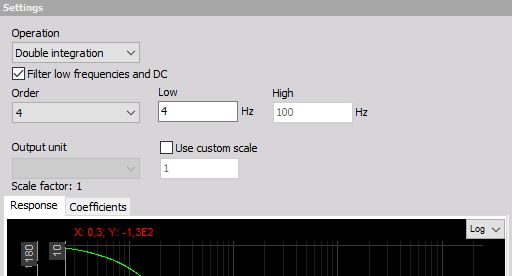
Double integration
Double integration is useful mainly to directly integrate displacement from acceleration, so to use it for dynamic signals. Our output unit will be multiplied with sec * sec. Therefore we need to again to choose the option to Filter low frequencies and DC, but we have to take care since the double integration is similar to second order filter, we need to choose Order 3 or higher for low-frequency filter.
Let’s see how to calculate the Scale - scaling factor. Usually, we want the measurement result in μm (micrometers). So we have to enter a scaling factor of:
1 g * sec * sec = 9,81 m/sec/sec * sec * sec = 9,81 m = 9,81E6 μm